この記事では，以下のBuchsbaum & Gottshalk (1983)の論文について簡単に紹介する．
- Buchsbaum, G., & Gottschalk, A. (1983). Trichromacy, opponent colours coding and optimum colour information transmission in the retina. Proceedings of the Royal Society of London. Series B. Biological Sciences, 220(1218), 89–113.
Buchsbaum & Gottshalk (1983)では，視覚系のRGCやLGNにおける錐体拮抗型細胞の機能的意義について，情報処理の効率性の観点から解析をしている．具体的には，L・M・S錐体の分光感度を持つ仮想のセンサが無作為な光刺激を受容した際に，その信号の主成分分析をした固有ベクトルが錐体拮抗型応答と対応することを示した．
論文図2は，L・M・S錐体の波長に対する感度を示した関数であり（Vos & Walraven, 1971），L錐体とM錐体の応答関数は非常に近いことが読み取れる．論文中では，L・M・S錐体の応答関数を $R(\lambda),G(\lambda),B(\lambda)$ と表記しているが，画像処理で用いられるRGBとの区別からこの記事では， $L(\lambda),M(\lambda),S(\lambda)$ と表記する．
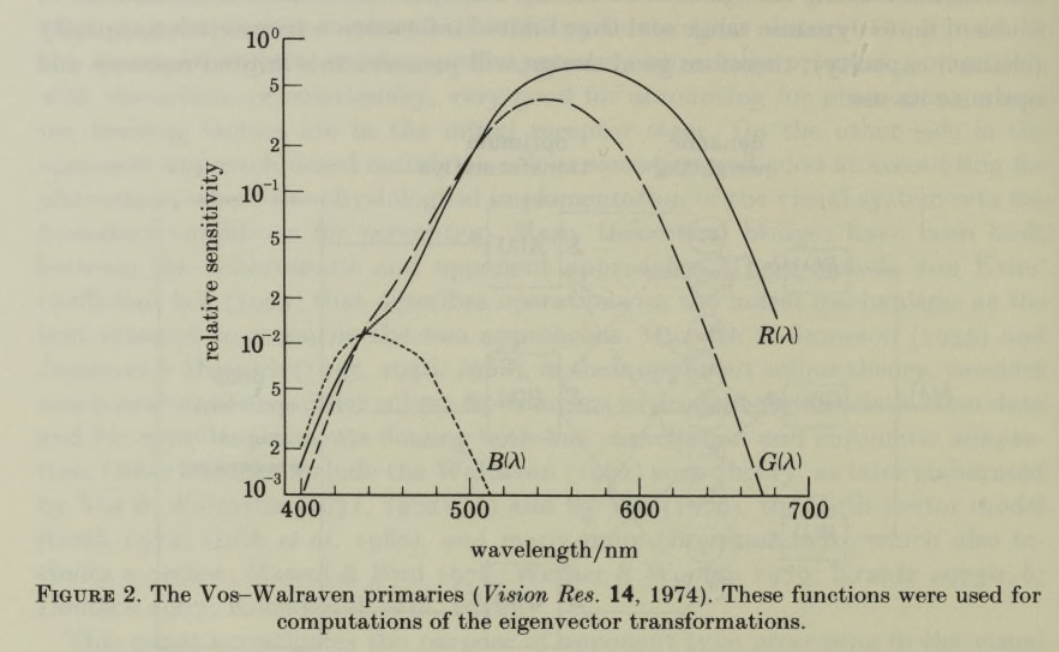(figure credit:
Buchsbaum & Gottshalk, 1983,
link to paper)
これらの波長 $\lambda$ に対する各錐体の応答関数 $L(\lambda),M(\lambda),S(\lambda)$ から，錐体応答量 $l,m,s$ は以下の式で計算することができる．
l = \int I(\lambda) L(\lambda) d\lambda, \quad m = \int I(\lambda) M(\lambda) d\lambda, \quad s = \int I(\lambda) S(\lambda) d\lambda.
ここで， $I(\lambda)$ は入力光の分光強度を意味しており，解析には $N$ 個の無作為な分光分布を持つ入力を用いている．Nx3の入力信号行列に対して，共分散行列を計算し，そこから固有値分解によって固有ベクトルを計算する．ここで得られる３つの固有ベクトルが，視覚系のRGCやLGNにおける輝度・色チャネルと対応していることをこの論文では示している．具体的に，計算によって得られた固有ベクトルによって錐体応答量 $l,m,s$ を線形変換すると以下のようになる．
\begin{bmatrix} A \\ P \\ Q \end{bmatrix} = \begin{bmatrix} 0.887 & 0.461 & 0.0009 \\ -0.46 & 0.88 & 0.01 \\ 0.004 & -0.01 & 0.99 \end{bmatrix} \begin{bmatrix} l \\ m \\ s \end{bmatrix}
$A$ は $l$ と $m$ の加算によって表現され輝度チャネルと対応している． $P$ は $l$ と $m$ の錐体応答量の差分によって表現される色チャネルと対応し， $Q$ はもうひとつのS錐体方向の色チャネルと対応する．この分解ではS錐体方向のチャネルにおける $l+m$ 成分が無いように見えるが，錐体の分光応答関数を別の研究で計測したもので計算すると(例：Smith & Pokorny, 1975)，S錐体応答とL+M錐体応答の相対感度が変化するため，3つめの固有ベクトルにL錐体，M錐体の寄与が現れる．
他にも論文では，錐体順応の影響や，2色型の錐体の影響について，主成分分析の観点から検討をしている．
以上のように，視覚系による錐体応答の変換が，錐体応答の冗長性を解消し，効率的な情報処理を行う機能的意義を持つということをこの研究では示している．